SECTION 4.2
205
Coordinate Systems
A transformation matrix in PDF is specified by six numbers, usually in the form
of an array containing six elements. In its most general form, this array is denoted
[
a b c d e f
]
; it can represent any linear transformation from one coordinate
system to another. This section lists the arrays that specify the most common
transformations; Section 4.2.3, “Transformation Matrices,” discusses more math-
ematical details of transformations, including information on specifying transfor-
mations that are combinations of those listed here:
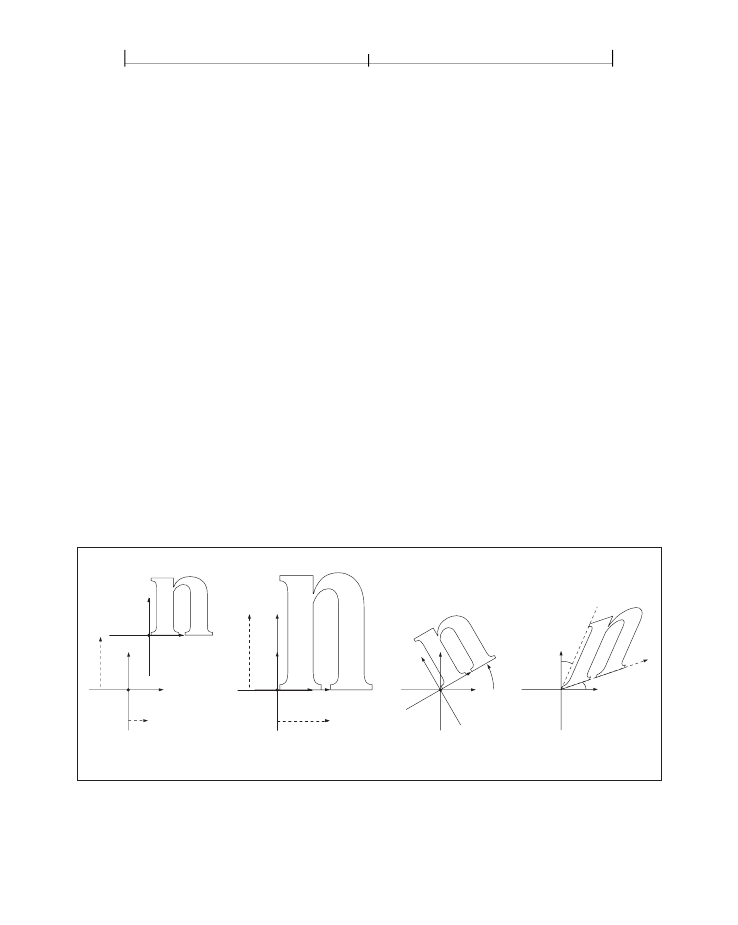
•
Translations are specified as
[ 1
•
Scaling is obtained by
[
s
x
0 0 1
t
x
t
y
]
, where
t
x
and
t
y
are the distances
to translate the origin of the coordinate system in the horizontal and vertical
dimensions, respectively.
0 0
s
y
0 0 ]
. This scales the coordinates so that 1
unit in the horizontal and vertical dimensions of the new coordinate system is
the same size as
s
x
and
s
y
units, respectively, in the previous coordinate system.
•
Rotations are produced by
[
cos
θ
sin
θ
−sin
θ
cos
θ
•
Skew is specified by
[ 1
tan
α
tan
β
α
and the
y
axis by an angle
β
.
of rotating the coordinate system axes by an angle
θ
counterclockwise.
0 0 ]
, which has the effect
1 0 0 ]
, which skews the
x
axis by an angle
rotation, and skew shown in the figure correspond to positive values of the array
elements.
t
y
s
y
q
b
a
t
x
s
x
Translation
Scaling
Rotation
Skewing
FIGURE 4.5
Effects of coordinate transformations